fibonacci คือ อะไร การใช้งานและการวิเคราะห์

Fibonacci คือ อะไร

ตัวเลข Fibonacci คือ ลำดับเลขในธรรมชาติที่เชื่อว่า แทรกซึมอยู่ในธรรมชาติทุกหนแห่ง มันมีการใช้ในคณิตศาสตร์ ด้านการเงิน ด้านฟิสิกข์ การคำนวณ หรือความสวยความงามอย่างกว้างขวาง

ตัวเลขของฟิโบนารี่ (Fibonacci Numbers) หรือ อันที่จริงควรจะเรียกว่า ลําดับของตัวเลขของฟิโบนาซี (Fibonacci Sequence) มากกว่า มันคือชุดของตัวเลขที่มีคุณสมบัติที่ใกล้เคียงกับสภาวะธรรมชาติ ที่พบเห็นได้โดยทั่วไป

• ตัวเลขเหล่านี้ เป็น ที่มาของสัดส่วนทองคํา (Golden Ratio)
• พบเห็นได้ในธรรมชาติ ไม่ว่าจะเป็นสิ่งมีชีวิต หรือ สถาปัตยกรรมอันทรงคุณค่า
• สัดส่วนทองคํานี้ ก็เป็นสิ่งหนึ่งที่นักวิเคราะห์ทางเทคนิคนํามาประยุกต์ใช้กับตลาดหุ้น หรือ Forex
• เนื่องจากสัดส่วนทองคํานี้เป็นองค์ประกอบของธรรมชาติ ดังนั้น เราจึงพบเห็นมันจนคุ้นเคย
• มันก็เลยกลายเป็นธรรมชาติอย่างหนึ่งของเราไป
• ซึ่งเป็นสาเหตุที่ว่า ทําไมเรา จึงจะพบสัดส่วนทองคํานี้ในตลาดหุ้นด้วย
• เพราะมันเป็นอะไรที่เราคุ้นเคย ดูแล้วสบายตา ใช้แล้วเพลินใจ
• บางครั้งเราก็ ประพฤติตนตามสัดส่วนทองคํานี้ด้วย
• เพียงแต่ว่าเราไม่ค่อยจะได้สังเกตมันเท่านั้นเอง
• แต่นักวิเคราะห์ทางเทคนิคที่เชื่อใน เรื่องของคลื่นอีเลียต (Eliott Wave) หรือ วงจรวัฏจักร (Cycles) ส่วนใหญ่แล้ว จะคุ้นเคยกับมันเป็นอย่างดี

ฟิโบนาชี่ คือใคร

ฟิโบนารี่ เขาคือ นักคณิตศาสตร์ชาวเมืองปิซ่า ประเทศอิตาลีครับ ชื่อเต็มของแกคือ ลิโอนาร์โด ฟิโบนารี่ (Leonardo Fibonacci)

• เกิดสมัยปลายคริสตศตวรรษที่ 12 ซึ่งจัดว่าเป็นยุคกลาง
• เพราะยุโรปเพิ่งเข้าสู่ยุคกลางสมัยคริสตศตวรรษ ที่ 11 ซึ่งจัดเป็นยุคฟื้นฟูศิลปะวัฒนธรรม หรือ Reneisance
• โดยเฉพาะอย่างยิ่งในเรื่องของวิชาคณิตศาสตร์ เพราะในยุคมืด (นับตั้งแต่ปลายคริสตศตวรรษที่ 5) นั่น คณิตศาสตร์ในยุโรปไปไม่ค่อยถึงไหนเท่าไหร่
• ช่วงนั้นคณิตศาสตร์ รุ่งเรืองสุดขีดในแถบอินเดียและอาราเบีย
• สาเหตุหนึ่งอาจจะ เป็นเพราะระบบตัวเลขของโรมันนไม่ได้ใช้เลขฐานสิบที่เราใช้กันอยู่ทุกวันนี้หรอกครับ
• โรมันใช้อักษร ประเภท I, II, III, IV, V แทน ซึ่งไม่เหมาะที่จะใช้ในการคํานวณ
• โชคยังดีที่ว่าเวลาคํานวณกันจริงๆ แล้ว พวกโรมันจะใช้ลูกคิดช่วยในการคิด ซึ่งลูกคิดนี่มีพื้นฐานอยู่บนเลขฐานสิบที่เราใช้กันอยู่ทุกวันนี้

กำเนิด Fibonacci

พ่อของฟิโบนาซีเป็นศุลการักษ์ ที่เมืองปิซ่าซึ่งเป็นเมืองท่าที่มีการค้าขายเจริญรุ่งเรืองมาก ดังนั้น ฟิโบนาชี่จึงค่อน ข้างจะคล่องเรื่องของการค้าขาย โดยเฉพาะการคํานวณโดยใช้ลูกคิด

นอกจากนี้เขายังสามารถพูดได้หลายภาษา ได้แก่

• ภาษาฝรั่งเศส
• กรีก
• ละติน

และความรู้ทางด้านคณิตศาสตร์ของเขาไปเพิ่มพูนอย่างสุดขีด ตั้งแต่สมัยที่พ่อได้รับแต่งตั้งให้ ไปประจําการที่อัฟริกาใต้ซึ่งส่งผลให้ฟิโบนารี่ได้เดินทางไปแถบทะเลเมดิเตอร์เรเนียนกับพ่อด้วย และได้ซึมซับ ระบบคณิตศาสตร์ประเภทเลขฐานสิบมาอย่างช่ำชอง

อิทธิพลต่อคณิตศาสตร์ยุโรป

เมื่อกลับมาอิตาลีแล้ว เขาได้เขียนหนังสือเล่มแรกชื่อ

“ตําราแห่งการคํานวณ” หรือ Liber Abaci (ภาษาอิตาเลี่ยนครับ แปลว่า Book of Calculation)

ซึ่งกลายเป็นพื้นฐานของการใช้เลข ฐานสิบระบบฮินดู-อาราบิคในยุโรป และส่งผลให้มีการใช้ระบบการคํานวณแบบนี้มาจนถึงปัจจุบัน

ความมีชื่อเสียงของ ฟิโบนักชี

ฟิโบนารี่เป็นคนมีชื่อเสียงพอสมควรในสมัยนั้น ขนาดพระเจ้าเฟรดเดอริกที่ 2 ซึ่งเป็นกษัตริย์ที่ทรงเป็นนักวิชาการคน สําคัญของยุคนั้น เสด็จมาดูตัว

เมื่อนักคณิตศาสตร์มาพบกัน ก็มีการถกเถียงและวิจารณ์ในเชิงวิชาการทางคณิตศาสตร์อย่างกว้างขวางตัวฟิโบนารี่เองก็ประทับใจมาก ขนาดที่ว่าตอนพิมพ์หนังสือ ตําราแห่งการคํานวณ ฉบับปรับปรุงเพิ่มเติมเป็นครั้งที่ 2 เขาตั้งชื่อฉบับนี้ว่า “ฉบับพระเจ้าเฟรดเดอริกที่ 2”

ฟิโบนารี่ ได้สร้างผลงานที่ทรงอิทธิพลต่อพื้นฐานทางคณิตศาสตร์ในยุคปัจจุบันอย่างมหาศาล แต่สุดท้ายแล้วกลับไม่ค่อยมีใครรู้จักเขาเท่าที่ควร นับเป็นที่น่าเสียดาย

แม้แต่ในอิตาลีเอง ก็มีเพียงถนนสองสาย (สายหนึ่งในเมือง ปิซ่า และอีกสายหนึ่งในเมืองฟลอเรนซ์) ที่ให้เกียรติใช้ชื่อถนนว่าฟิโบนารี่ และแถมด้วยอนุสาวรีย์อันเล็กๆอีกอันนึ่งในเมือง ปิซ่า ฟิโบนารี่เป็นนักคณิตศาสตร์ร่วมสมัยกับโบนานา (Bonana) ผู้ออกแบบสร้างหอเอนแห่งเมืองปิซ่า

แต่โบนานาผู้ซึ่ง ออกแบบหอคอยแล้วเอียงกระเท่เร่ กลับดังและมีคนรู้จักมากกว่า

ลำดับเลข Fibonacci

ลำดับเลข Fibonacci คือ ลำดับตัวเลขที่เกิดจากการรวมกันของตัวเลขปัจจุบันกับตัวเลขชุดก่อนหน้า โดยมีตัวอย่างการคำนวณ ดังต่อไนปี้

• 0+1=1
• 1+2=3
• 2+3=5
• 3+5=8
• 5+8=13
• 8+13=21
• 13+21=34
• 21+34=55
• 34+55=89

ทฤษฎีเกี่ยวกับ Fibonacci

ทฤษฎีเกี่ยวกับ Fibonacci มีกล่าวไว้ในตำราแห่งการคำนวณของเขา โดยเขายกตัวอย่างเกี่ยวกับกระต่ายและการขยายพันธ์ โดยมีตัวอย่างดังนี้

ตัวอย่างกระต่ายกับ Fibonacci

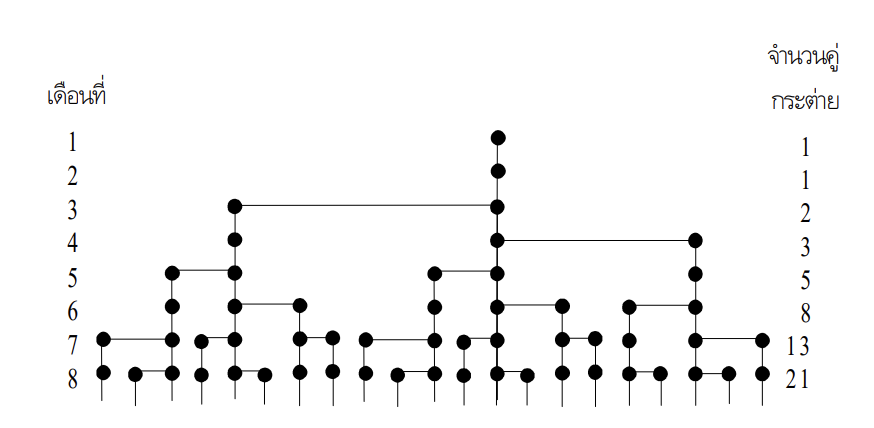
สมมุติว่า กระต่ายหนึ่งคู่ต้องใช้เวลา 1 เดือนถึงจะผสมพันธ์ได้ และใช้เวลาตั้งท้องนาน 1 เดือนจะมีลูกกระต่ายออกมา 1 คู่ ถ้าเราเอากระต่าย 1 คู่มาเลี้ยง ภายใน 1 ปีจะมีกระต่ายกี่ตัว

ปัญหา กลายเป็นที่มาของ ลำดับเลข Foibonacci ดังภาพข้างต้น และมีการคำนวณจำนวนเดือน โดย เดือนแรกมีกระต่าย 1 คู่ เพราะกระต่ายใช้เวลาท้อง 1 เดือน เดือนที่ 2 จึงยังมีแค่ 1 คู่

• ในเดือนที่ 3 จึงจะมีลูกกระต่ายออกมาอีก 1 คู่ รวมเป็น 2 คู่
• เดือนที่สี่ กระต่ายคู่แรกออกลูกมาได้อีก 1 คู่ แต่คู่ที่สองเพิ่ง ถึงวัยเจริญพันธุ์และกําลังตั้งท้องลูกครอกแรก ดังนั้นจึงมีกระต่าย 3 คู่
• ในเดือนที่ห้า ทั้งสองคู่สามารถออกลูกได้ ดังนั้น จึง มีกระต่าย 5 คู่ แบบนี้ไปเรื่อยๆ

ผังการเกิดของลูกกระต่าย แต่แสดงให้ดูแค่ 8 เดือนเพราะตั้งปี นึง ที่คงไม่พอเขียนแผนผัง จุดแต่ละจุดแทนจํานวนกระต่าย 1 คู่ เมื่อคํานวณแล้วจะพบว่าใน 1 ปี เราจะได้ลูก กระต่ายถึง 144 คู่

ถ้ากระต่ายไม่ตายเลย ภายใน 100 เดือน จะมีกระต่าย ทั้งหมด 354,224,848,179,261,915,075 คู่

ที่สําคัญคือจํานวนคู่ของกระต่ายที่มีในแต่ละ เดือน ตัวเลขเหล่านี้ คือลําดับตัวเลขของฟิโบนารี่ ถ้าสังเกตให้ดีจะพบว่า ตัวเลขในลําดับตัวเลขของฟิโบนารี่ เป็นผลรวมของตัวเลขก่อนหน้าตัวมันเอง 2 ตัวรวมกัน เช่น 1+1 ได้ 2, 1+2 ได้ 3, 2+3 ได้ 5, และ 3+5 ได้ 8 เป็นอย่างนี้

ในความเป็นจริง ถ้าเราจับเอาตัวเลขอะไรก็ได้มา 2 ตัว แล้วกําหนดให้ตัวที่สามเท่ากับ 2 ตัวแรกรวมกัน และตัวที่สี่เท่ากับตัวที่ สามบวกด้วยตัวที่สอง ตัวที่ห้าเท่ากับตัวที่สี่บวกด้วยตัวที่สาม เป็นเช่นนี้ไปเรื่อยๆ ก็จะเรียกลําดับของตัวเลขนี้ว่าลําดับตัว เลขของฟิโบนารี่เหมือนกัน แต่ที่นิยมกันก็คือใช้ 2 ตัวแรกเป็น 1 และ 1 อย่างในตัวอย่าง

คุณสมบัติของ Fibonacci

คุณสมบัติของ Fibonacci มีสมบัติที่น่าสนใจดังนี้

1. ตัวเลขฟิโบนารี่ 2 ตัวที่ติดกัน จะไม่มีค่าคูณร่วมน้อย (ครน.) อื่นนอกจาก 1 หรือ พูดอีกอย่างหนึ่งก็คือ ระหว่างตัวเลข ฟิโบนารี่ 2 ตัวที่ติดกัน จะไม่มี Common Factor เลย
2. เมื่อเลือกตัวเลขฟิโบนารี่ 10 ตัว เริ่มจากเลขตัวไหนในลําดับก็ได้ แต่ให้เรียงกันมา 10 ตัว นํามาบวกเข้าด้วยกัน ผลบวกที่ได้ จะสามารถหารด้วย 11 ได้ลงตัวเสมอ ตัวอย่างเช่น 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 + 89 + 144 = 374 ซึ่งหารด้วย 11 ลงตัวได้ 34
3. ตัวเลขฟิโบนาชี้ใดๆ หารด้วยตัวเลขที่อยู่ในลําดับถัดไป (Fi/F1) จะมีค่าเข้าใกล้ 0.618 ตัวอย่างเช่น 55 / 89 =0.618
4. ตัวเลขฟิโบนารี่ใดๆ หารด้วยตัวเลขที่อยู่ในลําดับก่อนหน้าของมัน (Fi/F-1) จะมีค่าเข้าใกล้ 1.618 ตัวอย่างเช่น 89 /55 = 1.618
5. ตัวเลขฟิโบนารี่ใดๆ หารด้วยตัวเลขที่อยู่ในลําดับถัดไป 2 ลําดับ (Fi/F+2) จะมีค่าเข้าใกล้ 0.382 ตัวอย่างเช่น 34 /89 = 0.382
6. ตัวเลขฟิโบนารี่ใดๆ หารด้วยตัวเลขที่อยู่ลําดับก่อนหน้าของมัน 2 ลําดับ (F/F6-2) จะมีค่าเข้าใกล้ 2.618 ตัวอย่างเช่น 89 / 34 = 2.618

ความสัมพันธ์ระหว่างชุดตัวเลข

ตัวเลข Fibonacci มีความสัมพันธ์กันดังนี้

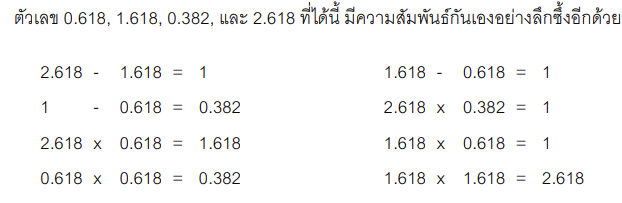
สัดสว่น 0.618, 1.618, 0.382, และ 2.618 เป็นสัดส่วนที่พบในธรรมชาติ โดยเฉพาะ 0.618 และ 1.618 ซึ่งเรียกว่า สัดส่วนทองคำ (Golden Ratio) ซึ่งเรียกว่า เป็นสัดส่วนที่น่าหลงไหลที่สุด

สัดส่วนทองคำกับธรรมชาติ

สัดส่วนทองคํานี้ ไม่ใช่เพิ่งมารู้จักกันในสมัยของฟิโบนาชื่ เราค้นพบสัดส่วนทองคํานี้มาตั้งนานแล้ว

พวกกรีกโบราณเรียกตัวเลขนี้ว่า ค่าเฉลี่ยทองคํา (Golden Mean) และใช้สัญญลักษณ์ 0 หรือที่เรียกว่า “ฟี” (Phi) เป็นตัว แทนสัดส่วน 1.618

เพลโต้ปรัญชาเมธีชาวกรีก เขียนไว้ในหนังสือ Timaeus ของเขาว่า สัดส่วน Phi นี้เป็น เสมือนตัวเชื่อมความสัมพันธ์ระหว่างคณิตศาสตร์ทั้งมวล และเป็นกุญแจสําคัญของฟิสิกส์ว่าด้วยเอกภพและจักรวาล

โครงสร้างของวิหารพาเธนอน (Pathenon) ของกรีก ตลอดจนปิรามิดแห่งเมืองกิซ่าของอียิปต์ ก็ถูกสร้างขึ้นมา โดยใช้สัดส่วนทองคํานี้

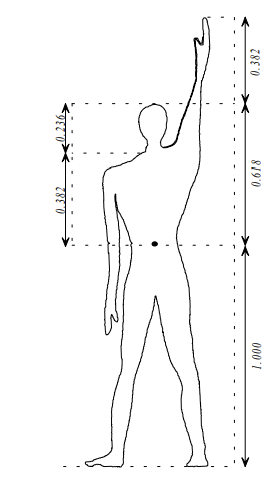
สัดส่วนทองคำกับร่างกายมนุษย์

เราจะเห็นสัดส่วนทองคํานี้ได้ในธรรมชาติทั่วไป เพียงแต่เราไม่ได้สังเกตเท่านั้น ตัวอย่างเช่น ร่างกายของคนเราก็ เป็นไปตามสัดส่วนทองคําครับ คนที่มีรูปร่างงดงาม จะมีสัดส่วนจากสะดือถึงหัว เมื่อเทียบกับจากสะดือถึงเท้าแล้ว เท่ากับ 0.618 พอดี ความยาวจากสะดือถึงหัวไหล่ของคนเราจะมีสัดส่วนเท่ากับ 0.382 เท่า ในขณะที่สัดส่วนจากหัวถึงปลายมือของเราจะมีสัดส่วนเท่ากับ 0.382 เท่าของความยาวจากสะดือไปยังปลายเท้าเช่นกัน

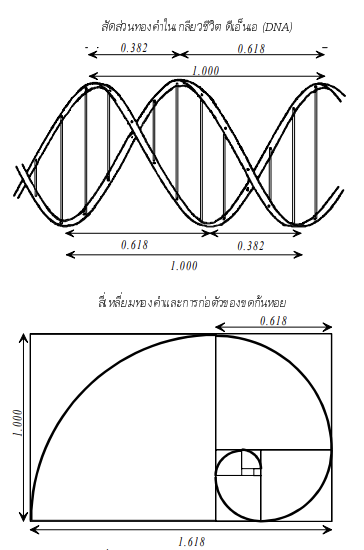
ก้นหอยและ DNA

แม้แต่ในส่วนที่เล็กที่สุดและมีความสําคัญต่อชีวิตที่สุด คือ ดีเอ็นเอ (DNA: Dioxy ribo-Nucleic Acid) ซึ่งเป็นองค์ประกอบสําคัญของสิ่งมีชีวิต (บางท่านเรียก DNA ว่า เกลียวชีวิต ) ก็เป็นไปตามสัดส่วนทองคําด้วย

สัดส่วนทองคําที่เห็นได้บ่อยที่สุด จะอยู่ในรูปของวงก้นหอยซึ่งวงก้นหอยนี้ สามารถสร้างได้ จากสี่เหลี่ยมผืนผ้าที่มีด้านยาวเป็น 1.618 เท่าของด้านกว้าง เราเรียกสี่เหลี่ยมนี้ว่า สี่เหลี่ยมทองคํา (Golden Rectangle) โดยเราสามารถสร้างสี่เหลี่ยมทองคําขนาดเล็กขึ้นจากสี่เหลี่ยมทองคําอันเดิมได้ไม่รู้จบ เมื่อโยงเส้นโค้งตามแนวทแยงมุม จะได้วงก้นหอยที่ขดตัวไม่รู้จบ

โดยวงก้นหอยนี้จะมีรัศมีที่ค่อยๆขยายตัวเป็นสัดส่วนเท่ากับ 1.618 และมีความยาวของเส้น รอบวงขยายตัวด้วยสัดส่วนเดียวกัน การขยายตัวแบบวงก้นหอยนี้ จะพบเห็นได้ทั่วไป เช่น ในเปลือกหอย, ลูกสน, เขาแกะ, หางม้าน้ํา, วังวนของกระแสน้ํา, การม้วนตัวของคลื่น, การหมุนตัวของพายุเฮอริเคน, และแม้แต่การขยายตัวของ เอกภพ ก็เป็นไปตามแบบแผนนี้ด้วยเช่นกัน

Fibonacci กับ การทำนายราคา

เมื่อเราเริ่มเข้าใจตัวเลขของฟิโบนารี่และสัดส่วนทองคํากันดีแล้ว เราก็จะเริ่มนําเอาสัดส่วนทองคํา ที่ได้จาก ตัวเลขของฟิโบนารี่ มาประยุกต์ใช้กับตลาดหุ้นกัน

โดยเราจะเริ่มจากการนําเอาสัดส่วน 0.618 และ 0.382 ตลอดจน 1 และ 1.618 มาใช้ในการคาดการณ์เป้าหมายของราคาหุ้น ว่าควรจะเข้าไปรับซื้อในช่วงไหน และราคาน่าจะวิ่งไปได้ถึง ระดับไหน ซึ่งเป็นเรื่องของการปรับฐาน หรือ การดีดตัว (Retracement) และการต่อตัว (Extension)

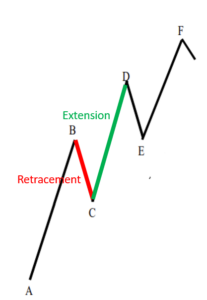
Retracement

เรามาทําความเข้าใจเกี่ยวกับคํานิยามของคําว่า การปรับฐาน หรือ การดีดตัว (Retracement) และ การต่อตัว (Extension) กันก่อนเพื่อให้เข้าใจตรงกัน จะได้ไม่สับสน ตามปกติเวลาตลาดหุ้นกําลังเป็นขาขึ้น การเคลื่อน ไหวของราคาก็ไม่ได้ขึ้นอย่างเดียวตะพึดตะพือ

แต่จะมีการปรับตัวอยู่ตลอดเวลา อย่างที่ภาษานักเล่นหุ้นเราเรียกว่าปรับ ฐานนั่นแหละครับ ก่อนที่จะวิ่งขึ้นต่อไปได้อีกส่วนในกรณีที่ตลาดเป็นขาลงก็เช่นเดียวกันก็มี การปรับฐาน โดยราคาจะดีดตัวขึ้นมา ก่อนที่จะอ่อนตัวลง

Extension

ในกรณีที่เป็นขาขึ้น การปรับฐานนี่ก็เป็นจุดหนึ่งสําหรับการเข้าไปรับซื้อ เพื่อหวังว่า ราคามันจะดีดตัวขึ้นต่อไป และเมื่อราคาดีดตัวขึ้นต่อไปจริงๆตามคาดแล้ว เราก็ ต้องตั้งเป้าไว้เหมือนกันว่าจะไปขายที่จุดไหน เป้าขายที่ตั้งไว้เราจะคํานวณจาก การต่อตัว (Extension) ซึ่งหมายถึงการที่ราคาเคลื่อนไหวต่อไปตามทิศทางของ แนวโน้มหลัก

ส่วนในกรณีขาลง จะกลับกัน กล่าวคือ การปรับฐานเป็นการดีดตัวขึ้นของราคา เป็นจุดที่จะตั้งขาย ในขณะที่การต่อตัวจะเป็นจุดที่เราคิดว่าราคาจะลงต่อไปอีก ตามแนวโน้มเดิม และเป้าที่ตั้งไว้ ก็จะเป็นเป้าซื้อที่นี้

ปัญหาที่ตามมาก็คือ เราควรจะตั้งเป้าอย่างไรว่า จุดปรับฐานจะอยู่ที่เท่าใด และจุดต่อตัวจะต่อไปได้ถึงแค่ไหน อันนี้ เราก็จะนําเอาสัดส่วนทองคํา ตลอดจนตัว เลขสัดส่วนต่าง ๆ ที่ได้จากตัวเลขของฟิโบนารี่มาใช้ในการหาเป้าหมายของราคา กันล่ะครับ การหาเป้าหมายของราคาในกรณีของการปรับฐาน เราเรียกว่า

Fibonacci Retracement ซึ่งเป้าหมายแต่ละจุดที่คํานวณได้นี้ เราเรียกว่า ปมของฟิโบนาชี่ หรือ FibNode ส่วนเป้า หมายของราคาในกรณีของการต่อตัว

เราเรียกว่า Fibonacci Extension โดยแต่ละจุดของเป้าหมายราคาที่คํานวณจากการต่อตัวนี้ เราจะเรียกว่า ราคาเป้าหมาย (Objective Price)

Fibonacci Retracement

Fibonacci Retracement เป็นการวัดเป้าหมายว่า ราคาจะปรับฐานลงไปลึกเท่าใด (ในกรณีที่แนวโน้มหลักเป็นขาขึ้น) หรือจะดีดตัวขึ้นสูงเพียงใด (ในกรณีที่แนวโน้มหลักเป็นขาลง)

• รูปแสดงการคํานวณเป้าหมายของการปรับฐาน ราคา ทั้งในกรณีที่แนวโน้มเดิมเป็นขาลง และในกรณีที่แนวโน้มเดิมเป็นขาขึ้น
• ในกรณีที่แนวโน้มหลักเป็นขาลง การปรับฐานก็คือการดีดตัวสูงขึ้นของราคา ซึ่งเป้าหมายว่าจะดีดตัวสูงขึ้นได้มากน้อย เพียงใดนั้น
• วัดจากจุดยอดเดิมเมื่อครั้งที่มีการดีดตัวคราวที่แล้ว ไปยังจุดต่ํา สุดก่อนที่ราคาจะดีดตัวขึ้น

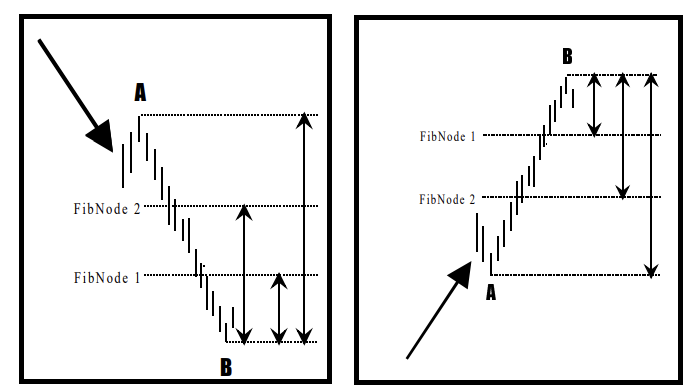
การดู Fibonacci Retracement

การดู Fibo เชื่อว่าราคาจะดีดตัวสูงขึ้นได้ 2 ระดับ ระดับแรกคือ 0.382 เท่าของระยะทางจาก B ไป A และระดับที่สองเท่ากับ 0.618 เท่าของระยะทางจาก B ไป A ซึ่งเราเรียกระดับแรก ว่า FibNode 1 และระดับที่สองว่า FibNode 2 ในกรณีที่แนวโน้มหลักเป็นขาลงนี้ FibNodes จะทําหน้าที่เป็น Resistance หรือ เป้าหมายในการขายทิ้ง สําหรับการเก็งกําไรในระยะสั้น

• ในกรณีที่แนวโน้มหลักเป็นขาขึ้น ก็คํานวณเหมือนๆกัน
• เราวัดจากจุดต่ําสุดเมื่อราคาปรับฐานคราวที่แล้ว ไปยังจุดสูงสุดก่อนที่ราคาจะปรับฐานครั้งล่าสุดเป้าหมายแรก หรือ FibNode 1 จะเท่ากับ 0.382 ของระยะทางจาก B ไปยัง A
• เป้าหมายที่สอง หรือ FibNode 2 จะเท่ากับ 0.618 เท่าของราคาจาก B ไปยัง A ในกรณีที่แนวโน้มหลักเป็นขาขึ้นนี้ FibNodes จะทําหน้าที่เป็น Support ซึ่งเป็นเหมือนกับแนวรับ สําหรับซื้อไว้เก็ง กําไรระยะสั้นๆ

Fibo Node 1 และ Node 2

ตัวอย่างการคํานวณ FibNodes 1 และ 2 กันดีกว่านะครับ จะได้เข้าใจดียิ่งขึ้น ตัวอย่างของเราแสดงอยู่ในรูปนี้ สมมติไว้ว่าเป็นกรณีที่แนวโน้มหลักเป็นขาลง และตอนนี้ราคากําลังดีดตัวขึ้นเพื่อปรับฐาน ก่อนที่ จะลงต่อไป ราคาได้ดีดตัวสูงขึ้นถึง 60 บาทในการปรับฐานคราวก่อน ก่อนที่จะตกลงมาตามแนวโน้มหลักเหลือ 30 บาท

แล้วกําลังดีดตัวขึ้นอีกครั้งหนึ่ง ในกรณีนี้ ราคาระหว่าง B ไปยัง A ก็เท่ากับ 60-30 = 30 บาท

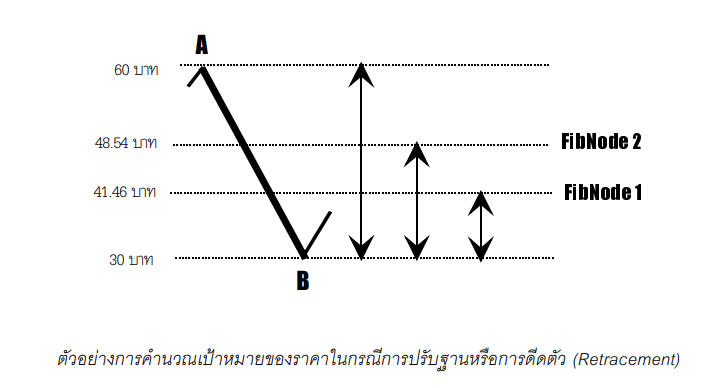
ดังนั้น เป้าหมายแรกของ การดีดตัว ก็คาดว่าจะดีดตัวขึ้น 30 x 0.382 = 11.46 บาทสูงขึ้นกว่าจุด B ดังนั้น เป้าหมายแรก หรือ FibNode 1 ก็เท่ากับ

30 + 11.46 = 41.46 บาท

สําหรับเป้าหมายที่สอง หรือ FibNode 2 นั้น ก็คํานวณแบบเดียวกัน เพียงแต่ใช้ Golden Ratio คือ 0.618 แทน เราจะได้ FibNode 2 เท่ากับ 30 x 0.618 + 30 = 48.54 บาท

หลายคนอาจจะสงสัยว่า เมื่อเป้าหมายของการปรับฐานหรือการดีดตัว (Retracement) นี้มันมี 2 อัน คือ FibNode 1 และ FibNode 2 แล้วเราจะเชื่ออันไหนดีล่ะ

• คําตอบก็คือ ขึ้นอยู่กับสถานการณ์
• เช่น การดีดตัวหรือการปรับฐานนี้ มีปริมาณการซื้อขายหนาแน่นเพียงใด
• ถ้ามีปริมาณการซื้อขายที่หนาแน่นรองรับอยู่ด้วย FibNode 1 ก็อาจจะรับไม่อยู่ มีโอกาสที่จะวิ่งไปถึง FibNode 2 ได้มากพอควร
• เราอาจจะพิจารณาควบคู่ไปกับแนว รับแนวต้านอื่นๆ จากวิธีการวิเคราะห์ทางเทคนิคแบบต่างๆ ถ้าหาก FibNode ไหนที่มีแนวรับแนวต้านจากเครื่องมือทาง เทคนิคอื่นๆ เสริมด้วย FibNode นั้น ก็จะมีนัยสําคัญมากขึ้น

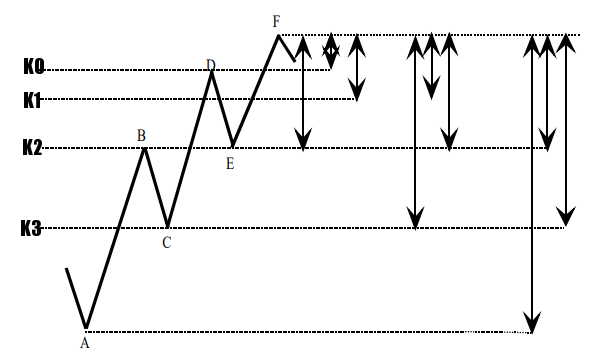
อีกกรณีหนึ่งก็คือ ถ้า FibNode นั้น ได้รับแรงสนับสนุนจาก FibNode อื่น เมื่อวัดจากยอดต่างๆของการปรับฐานในอดีต ก็ จะทําให้ FibNode นั้น น่าเชื่อถือยิ่งขึ้น ฟังแล้วอาจจะงง

ลองดูตัวอย่างในรูปข้างบนดีกว่าจะเข้าใจได้ดียิ่งขึ้น เราจะเห็นว่าเป้าหมายที่ระดับ K1 และ K2 มีนัยสําคัญมากกว่าเป้าหมายที่ระดับอื่นๆ เพราะทั้ง K1 และ K2 ต่างก็เป็น ระดับที่มีแรงเสริมจาก Fibonacci Retracement Ratio มากกว่า 1 ครั้ง ตัวอย่างเช่น ที่ K1 นั้น มี Fibonacci Retracement Ratio อยู่ 2 อัน คือ 0.618 ของช่วง EF และ 0.382 ของช่วง CF

ในกรณีของ K2 ก็เป็นจุดที่มีนัยสําคัญมาก อาจจะเรียกได้ว่าเป็นจุดที่มีนัยสําคัญมากที่สุดในรูปนี้เลยก็ได้ เพราะเป็นจุดที่ ได้รับแรงหนุนจากจุดต่ําสุด (trough) เดิม คือ จุด E นอกจากนั้น ยังมี Retracement Ratio อีก 2 ระดับ คือ 0.618 ของ ระยะ CF และ 0.382 ของระยะ AF

Fibonacci Extension

การเกิด Extension คือ การเคลื่อนไหวของราคาไปตามทิศทางของแนวโน้มหลัก ดังแสดงในรูป A และ B ซึ่งใน

กรณีของรูป

• A นั้น แนวโน้มหลักเป็นขาขึ้น ซึ่งหลังจากที่ปรับฐานแล้ว ก็พยายามวิ่งขึ้นต่อไปในทิศทางแนวโน้มหลัก
• ส่วนในรูป B นั้น แนวโน้มหลักจะเป็นขาลง

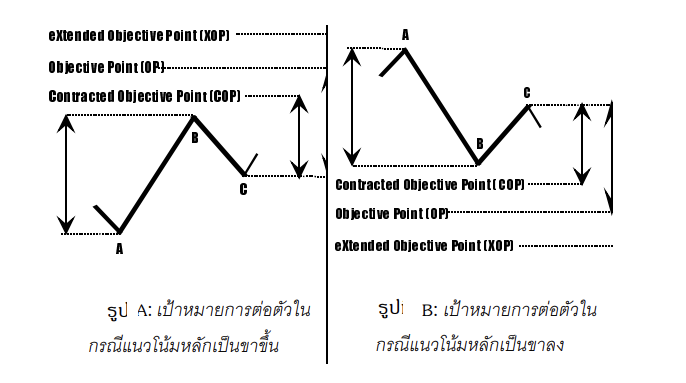
เป้าหมายของราคา

Target ของราคาในกรณีของการต่อตัวนั้น แบ่งออกเป็น 3 เป้าด้วยกันคือ

1. เป้าหมายสั้น (Contracted Objective Point) หรือ COP ซึ่งคํานวณจาก 0.618 เท่าของระยะราคาจาก A ไปยัง B
2. เป้าหมายปกติ (Objective Point) หรือ OP คํานวณจากระยะราคาจาก A ไป B กล่าวคือ เคยขึ้นมาได้เท่าไร ขึ้นต่อไป ได้อีกเท่านั้น
3. เป้าหมายขยายตัว (Extended Objective Point) หรือ XOP คํานวณจาก 1.618 เท่าของระยะราคาจาก A ไปยัง B

การที่จะเลือก ว่าเป้าหมายใดเป็นเป้าหมายที่เหมาะสม ต้องพิจารณาความแรงของตลาดเป็นสําคัญ

ตามปกติแล้ว เป้า หมายปกติ หรือ OP นั้น จะถูกพบเห็นได้บ่อยกว่าเพื่อน ในขณะที่ COP จะถูกพบเห็นน้อยลงมา และ XOP จะถูกพบเห็น น้อยที่สุด แต่ทั้งนี้และทั้งนั้น ก็ขึ้นอยู่กับภาวะตลาดด้วย

กล่าวคือ ถ้าหากตลาดขึ้นมาเป็นระยะเวลานานแล้ว และกําลัง ของตลาดก็เริ่มอ่อนตัวลง (อาจจะสังเกตดูได้จากเครื่องมือทางเทคนิคประเภท Indicators เช่น RSI ซึ่งในกรณีที่ตลาดจะ หมดแรงแล้ว มักจะเกิด Divergence) ในกรณีเช่นนี้ cOP อาจจะมีนัยสําคัญมากกว่า OP ในทํานองกลับกัน

ถ้าตลาดเพิ่ง เริ่มเข้าสู่ภาวะกระทิง และตลาดมาแรงมาก (อาจจะสังเกตจากสัญญาณอื่นๆ เช่น เกิด Breakaway Gap หรือ ราคาทะลุ Moving Average Channel โดยสร้างความชันที่สูงกว่าเดิม) ในกรณีนี้ เป้าหมายอาจจะไปได้ถึงระดับ XOP เลยก็ได้

การคำนวณ COP, OP, XOP

การคํานวณ COP, OP, และ XOP ดังแสดงไว้ในรูป สมมติว่า แนวโน้มหลักเดิม เป็นขาขึ้น โดยจุดปรับตัวคราวก่อน (จุด A) อยู่ที่ระดับ 30 บาท และราคาได้ดีดตัวสูงขึ้นมาถึงจุด B คือ 60 บาท ก่อนที่จะมีการปรับฐานอีกครั้งที่จุด C ณ ระดับราคา 50 บาท จะสังเกตได้ว่า ในกรณีของการคํานวณเป้าหมาย ของราคาในกรณี Extension นั้น จะต้องใช้ 3 จุด คือ A, B, และ C ซึ่งต่างจากการคํานวณเป้าหมายของราคาในกรณีของ การปรับฐาน ที่ใช้แค่ 2 จุด คือ A และ B เท่านั้น

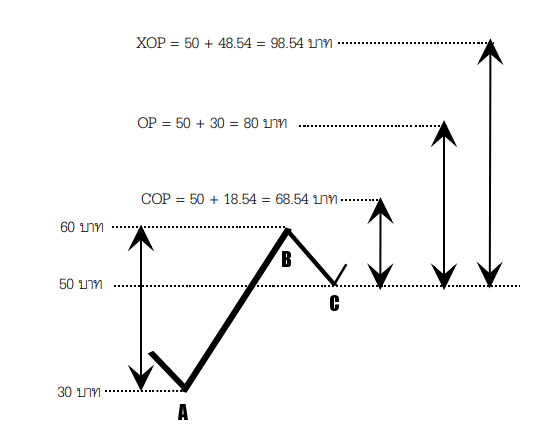
ในกรณีตัวอย่างนี้ ระยะราคาจาก A ไป B เท่ากับ 60 – 30 = 30 บาท ดังนั้น COP จะอยู่เหนือจุด C ขึ้นไปเท่ากับ 0.618 x 30 = 18.54 บาท หมายความว่า COP จะอยู่ที่ 50 + 18.54 = 68.54 บาท เช่นเดียวกัน OP ก็จะอยู่ที่ 50 + 30 = 80 บาท และ XOP จะอยู่ที่ระดับ 50 + 1.618 x 30 = 98.64 บาท

ข้อควรระวังเกี่ยวกับการใช้ Fibonancci

ในการคํานวณเป้าราคาต่างๆ ในที่นี้ เรามีข้อสมมติที่สําคัญอยู่อันหนึ่งว่า แนวโน้มหลักที่เป็นอยู่จะไม่เปลี่ยนแปลง

• เช่น ถ้า แนวโน้มหลักเป็นขาขึ้น เราก็คาดว่าจะขึ้นต่อไป
• ในความเป็นจริงแล้ว ก็จะต้องมีกรณีของการเปลี่ยนแนวโน้ม (Reversal) เข้ามาเกี่ยวข้องด้วย
• เพราะคงไม่มีหุ้นตัวไหนที่ราคาขึ้นแล้วไม่มีวันตกเลย
• ซึ่งถ้าเราคํานวณเป้าราคาตั้งรับใน ตอนปรับฐาน แล้วเข้าไปรับซื้อไว้
• แต่ปรากฏว่าราคากลับไม่ดีดตัวขึ้น แต่กลับตกลงไปอีก

เราจะต้องตรวจสอบทันทีว่า ราคาที่ตกลงไปอีกนี้ มันได้เปลี่ยนทิศทางของแนวโน้มหลักหรือยัง การวัดการเปลี่ยนแนวโน้ม อาจจะวัดได้จาก เครื่องมือ ทางเทคนิคที่เป็น Trend Reversal

เช่น เส้นค่าเฉลี่ยเคลื่อนที่ หรือ รูปแบบประเภท Head and Shoulder, Double และ Triple Top เป็นต้น

ถ้าพบว่าแนวโน้มหลักได้เปลี่ยนไปแล้ว เราจะต้องยอมตัดขาดทุนทันที อย่ารีรอเป็นอันขาด เมื่อเหตุ การณ์ไม่เป็นดังคาด เราจะต้องกล้าหาญพอที่จะยอมรับว่าเราผิดพลาดไปแล้ว และรีบแก้ไขปัญหาทันที อันนี้เราเรียกว่า เป็นการหยุดขาดทุน (Stop Loss)

forexduck

FOREXDUCK (นามปากกา) นักเขียนของเรามีประสบการณ์การเงินการลงทุนกว่า 10 ปี มีความเชี่ยวชาญในการวิเคราะห์ตลาด Forex และคริปโต โดยเฉพาะการวิเคราะห์ทางเทคนิค รวมถึงเทคนิคต่าง